Mohamed Anwar

I'm an ex-AI research resident at Meta

Also, I review research papers in these topics:

3 mins read

Published by: Google Research & Toyota Technological Institute at Chicago

ALBERT

ALBERT, stands for “A Lite BERT”, reduced version of BERT which is a smaller, faster, cheaper and easier to scale. ALBERT was created by Google & Toyota Technical Institute in February 2019 and published in this paper: “ALBERT: A Lite Bert For Self-Supervised Learning Of Language Representations” and you can fine the official code for this paper in Google Research’s official GitHub repository: google-research/ALBERT.

ALBERT incorporates two parameter reduction techniques that act as a form of regularization that stabilizes the training and helps with generalization; and one new loss function:

  • Factorized Embedding Parameterization

  • Cross-layer Parameter Sharing

  • Sentence-Order Prediction Loss

Also, The parameter reduction techniques also act as a form of regularization that stabilizes the training and helps with generalization.

These three modifications significantly reduce the number of parameters for BERT without seriously hurting performance. An ALBERT configuration similar to BERT-large has 18x fewer parameters and can be trained about 1.7x faster as shown in the following table:

And since longer training usually leads to better performance, the following table shows a comparison between the performance BERT and ALBERT after the same training time which shows that ALBERT still performs better:

Factorized Embedding Parameterization

In BERT, the Word embedding size $E$ is tied with the hidden layer size $H$, i.e., $E\ \equiv \ H$. This decision appears sub-optimal for the following reasons:

  • Word embeddings are meant to learn context-independent representations, whereas hidden-layer embeddings are meant to learn context-dependent representations. And that dictates that $H \gg E$.

  • NLP usually requires the vocabulary size $V$ to be large. If $E \equiv H$, then increasing $H$ increases the size of the embedding matrix, which has size $V \times E$. This can easily result in a model with billions of parameters, most of which are only updated sparsely during training.

So, instead of projecting the one-hot vectors directly into the hidden space of size H, they first projected them into a lower dimensional embedding space of size E, and then projected it to the hidden space. By using this decomposition, we reduce the embedding parameters from $O(V \times H)$ to $O\left( \left( V \times E \right) + \left( E \times H \right) \right)$. This parameter reduction is significant when $H \gg E$.

Cross-layer Parameter Sharing

The default decision for ALBERT is to share all parameters across layers. The following figure shows the L2 distances and cosine similarity of the input and output embeddings for each layer. We observe that the transitions from layer to layer are much smoother for ALBERT than for BERT.

These results show that weight-sharing has an effect on stabilizing network parameters. Although there is a drop for both metrics compared to BERT, they nevertheless do not converge to 0 even after 24 layers.

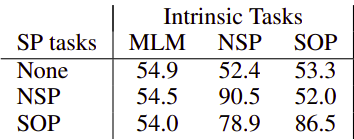
Sentence-Order Prediction (SOP)

In this paper, they proposed a new loss function called sentence-order prediction (SOP) loss as a replacement for next sentence prediction (NSP) used with BERT. The same as NSP, SOP loss uses two consecutive segments from the same document as a positive example. And as negative examples, it uses the same two consecutive segments but with their order swapped.

This forces the model to learn finer-grained distinctions about discourse-level coherence properties. As shown in the following table, it turns out that NSP cannot solve the SOP task at all, while SOP can solve the NSP task to a reasonable degree.

Hyper-parameters

In this part, we are going to talk about the effect of some hyper-parameters on ALBERT:

  • Network Depth (number of layers):
    If we compare a 3-layer ALBERT model with a 1-layer ALBERT model, although they have the same number of parameters, the performance increases significantly. However, there are diminishing returns when continuing to increase the number of layers: the results of a 12-layer network are relatively close to the results of a 24-layer network, and the performance of a 48-layer network appears to decline.
  • Network Width (hidden size):
    Using a 3-layers ALBERT, we can see that as we increase the hidden size, we get an increase in performance with diminishing returns. At a hidden size of 6144, the performance appears to decline significantly:
  • Dropout:
    Using ALBERT-xxlarge at around 1M training steps states that removing dropout helps the downstream tasks which indicates that ALBERT models didn’t overfit the data.
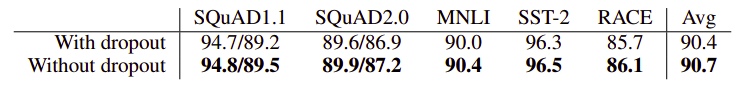
  • Data:
    Adding more data improvements on the downstream tasks, except for the SQuAD benchmarks (which are Wikipedia-based, and therefore are negatively affected by out-of-domain training material).