DistilBERT

DistilBERT is a smaller, faster, cheaper and lighter version of BERT created by Hugging Face in March 2020 and published in this paper: “DistilBERT, a distilled version of BERT: smaller, faster, cheaper and lighter”. In this paper, they used knowledge distillation to reduce the size of a BERT by 40%, while retaining 97% of its language understanding capabilities and being 60% faster. This was possible by using a triple loss function that combines language modeling, distillation and cosine-distance losses.

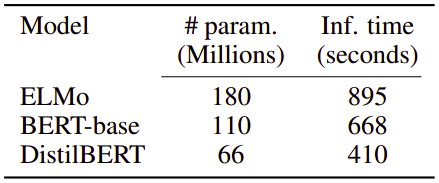
The following figure shows a simple comparison between DistilBERT and other models with respect to the number of parameters; which shows that DistilBERT is small enough to run on the edge, e.g. on mobile devices.

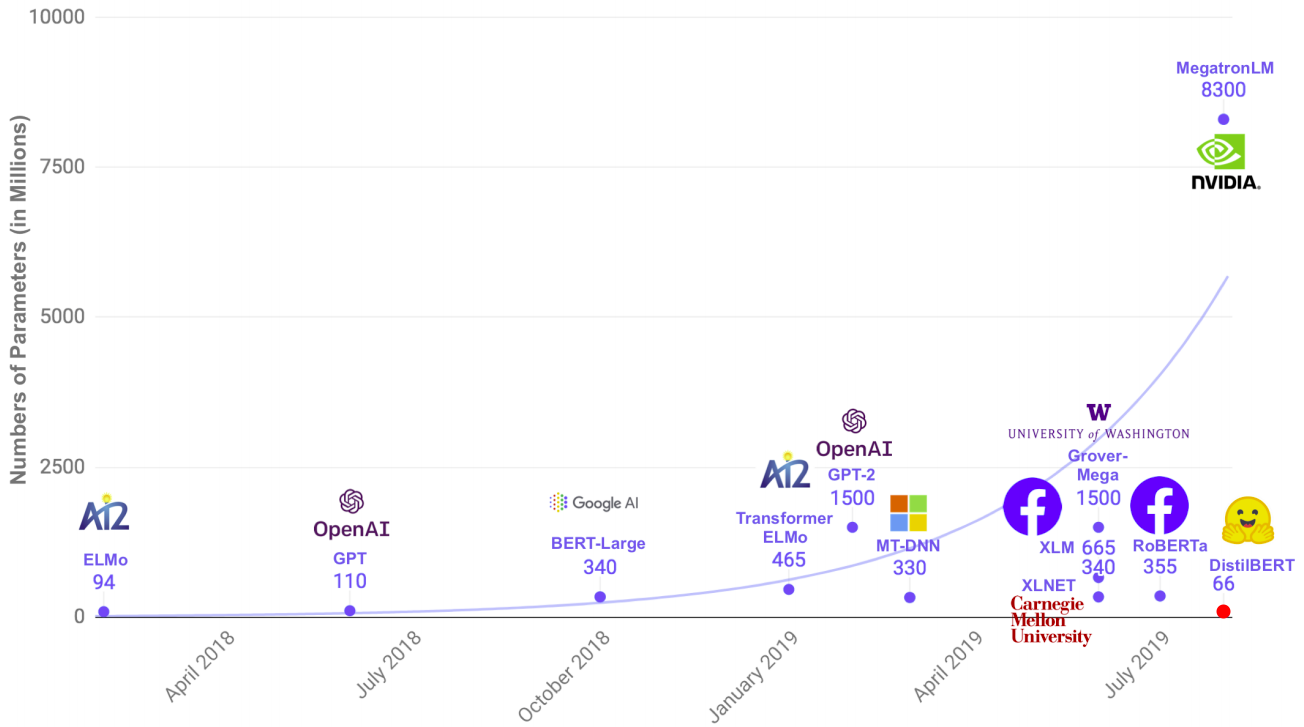
Knowledge Distillation

Knowledge distillation is a compression technique in which a compact model (the student) is trained to reproduce the behaviour of a larger model (the teacher). The teacher is trained on the hard labels (labels that belongs to one class) while the student is trained on soft labels (the class probabilities) which resulted from the teacher. In other words, the teacher is trained on the true labels from the training data and results probabilities that will be used to teach the student.

Triple Loss

In this paper, the student (DistilBERT) is trained with a triple loss which is a linear combination of three different losses which are:

$\mathcal{L}_{\text{ce}}$:
a distillation loss over the soft target probabilities of the teacher (BERT) where $t_{i}$ is the probability estimated by the teacher and $s_{i}$ is the probability estimated by the student.

\[\mathcal{L}_{\text{ce}} = \sum_{i}^{}{t_{i}\text{.log}\left( s_{i} \right)}\]

Calculating the probability ($t_{i}$ and $s_{i}$) is done using the softmax-temperature function where T is the temperature that controls the smoothness of the output distribution knowing that the same temperature will be used for the student and the teacher:

\[p_{i} = \frac{\exp\left( \frac{z_{i}}{T} \right)}{\sum_{j}^{}{\exp\left( \frac{z_{j}}{T} \right)}}\]

$\mathcal{L}_{\text{MLM}}$:
a masked language model loss; the same as BERT where ${\widehat{x}}{i}$ is the predicted word and $x{i}$ is the true word.

\[\mathcal{L}_{\text{MLM}}\left( x_{i} \right) = - \log\left( {\widehat{x}}_{i} \middle| x_{i} \right)\]

$\mathcal{L}_{\cos}$:
a cosine embedding loss which will tend to align the directions of the student and teacher hidden states vectors.

Architecture

The student (DistilBERT) has the same general architecture as BERT with these changes:

The token-type embeddings and the pooler are removed.
The number of layers is reduced by a factor of 2.
Most of the operations used in the Transformer architecture (linear layer and layer normalisation) are highly optimized in modern linear algebra frameworks.
Taking advantage of the common dimensionality between teacher and student networks, they initialized the student from the teacher by taking one layer out of two.
Following best practices, they used a very large batches (up to 4K examples per batch) using dynamic masking and without the next sentence prediction (NSP) objective.

And to show how efficient that was, let’s look on a simple comparison between DistilBERT and BERT on GLUE:

As we can see, DistilBERT retains 97% of BERT’s performance while being 40% smaller and 60% faster as shown in the following table: