Mohamed Anwar

I'm an ex-AI research resident at Meta

Also, I review research papers in these topics:

2 mins read

Published by: University of Montreal

Neural N-gram Language Model

As we discussed before, the n-gram language model has a few problems like the data sparsity and the big storage need. That’s why these problems were first tackled by Bengio et al in 2003 and published under the name “A Neural Probabilistic Language Model”, which introduced the first large-scale deep learning for natural language processing model. This model learns a distributed representation of words, along with the probability function for word sequences expressed in terms of these representations. The idea behind this architecture is to deal with the language model task as if it is a classification problems where:

  • The input is a window-sized subset of the previous tokens.

  • The output is the current token which could be any token from the vocabulary $V$.

  • Each token is represented using a one-hot vector.

  • The loss function is the cross entropy.

The following figure shows a simplified version of the neural network architecture that was created by Yoshua Bengio in 2003. In the original version of the model, Bengio used the input word vectors with both the hidden layer and the output layer. This simplified version concatenated word embeddings for the input words: $e = \left\lbrack e^{\left( 1 \right)};e^{\left( 2 \right)};e^{\left( 3 \right)};e^{\left( 4 \right)} \right\rbrack$, the red layer signifies the hidden layer: $h = f\left( We + b_{1} \right)$ , and the green output distribution is a softmax over the vocabulary: $ŷ = \text{softmax}\left( Uh + b_{2} \right)$.

And despite this model is way faster than other models and simpler to implement, there were still some problems that need to be fixed:

  • The fixed window is still a problem since some sentences need bigger windows to catch the context. So, no matter how big your window is, it will never be enough for some sentences.

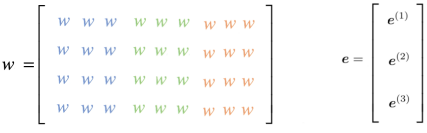
  • $e^{\left( 1 \right)},e^{\left( 2 \right)}$, … etc. are multiplied by completely different weights in W which means that the weight learning in one section is not shared with the others and that’s counter-intuitive. As shown in the following figure, we can see that $e^{\left( 1 \right)}$ will only by multiplied by the blue region of the weight matrix $W$, and $e^{\left( 2 \right)}$ will be only multiplied by the green region, and so on.