SpanBERT
SpanBERT is a model created by Facebook AI and Allen Institute in January 2019 and published in this paper “SpanBERT: Improving Pre-training by Representing and Predicting Spans”. SpanBERT is just an extension to BERT where it better represents and predict continuous random spans of text, rather than random tokens. This is crucial since many NLP tasks involve spans of text rather than single tokens. SpanBERT is different from BERT in both the masking scheme and the training objectives:
-
Span Masking:
SpanBERT masks random contiguous spans, rather than random individual tokens which forces the model to predict entire spans solely using the context in which they appear. -
SBO:
SpanBERT uses a novel span-boundary objective (SBO) so the model learns to predict the entire masked span from the observed tokens at its boundary which encourages the model to store this span-level information at the boundary tokens, which can be easily accessed during the fine-tuning stage. -
No NSP:
SpanBERT doesn’t use the NSP objective unlike BERT.

Span Masking
Given a sequence of tokens X, they selected a subset of tokens by iteratively sampling spans of text until the masking budget (e.g. 15% of X) has been spent. And they following the following steps when masking a subset of tokens:
- They randomly sample a span length (number of words) from a geometric distribution $\ell \sim Geo(p) = p.\left( 1 - p \right)^{n - 1}$ where $p = 0.2$ and $\ell_{\max} = 10$ which is skewed towards shorter spans as shown in the following figure. :
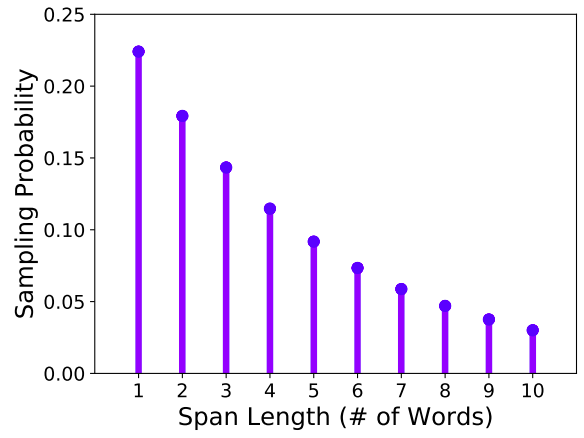
-
Then, they randomly select the starting point for the span to be masked from a uniform distribution. They always sample a sequence of complete words (instead of subword tokens) and the starting point must be the beginning of one word.
-
As in BERT, they also masked 15% of the tokens in total: replacing 80% of the masked tokens with [MASK], 10% with random tokens and 10% with the original tokens.
SBO
Span selection models typically create a fixed-length representation of a span using its boundary tokens (start and end). To support such models, we would ideally like the representations for the end of the span to summarize as much of the internal span content as possible. We do so by introducing a Span Boundary Objective (SBO) that involves predicting each token of a masked span using only the representations of the observed tokens at the boundaries.
Formally, they calculated the SBO loss function by following these steps:
-
Given an input sequence of $X = x_{1},\ …,\ x_{n}$ and a masked span of tokens $\left( x_{s},…,\ x_{e} \right) \in Y\ $, where $\left( s,\ e \right)$ indicates its start and end positions respectively.
-
They represented each token $x_{i}$ in the span using the output encodings of the external boundary tokens $x_{s - 1}$ and $x_{e + 1}$, as well as the position embedding of the target token $p_{i - s + 1}$:
- Then, they implemented the representation function as a 2-layer feed-forward network with GeLU activations and layer normalization
- Finally, they used the vector representation $y_{i}$ to predict the token $x_{i}$ and compute the cross-entropy loss exactly like the MLM objective.
For example, given the following sequence “Super Bowl 50 was an American football game to determine the champion” where the span “an American football game” is masked. The span boundary objective (SBO) uses the output representations of the boundary tokens, x4 and x9 (in blue), to predict each token in the masked span.

The equation shows the MLM and SBO loss terms for predicting the token, football (in pink), which as marked by the position embedding $p_{3}$, is the third token from $x_{4}$.
\[\mathcal{L}\left( \text{football} \right) = \mathcal{L}_{\text{MLM}}\left( \text{football} \right) + \mathcal{L}_{\text{SBO}}\left( \text{football} \right) = - log\ P\left( \text{football} \middle| \ x_{7} \right) - log\ P\left( \text{football} \middle| \ x_{4},x_{9},p_{3} \right)\]