Mohamed Anwar

I'm an ex-AI research resident at Meta

Also, I review research papers in these topics:

3 mins read

Published by: Carnegie Mellon University & Google Brain

Transformer-XL

Transformer-XL, stands for “Transformer Extra Long”, is a language model published in this paper: “Transformer-XL: Attentive Language Models Beyond a Fixed-Length Context” by Google Brain in 2019.The official code for this paper can be found in the following GitHub repository: transformer-xl .

In this paper, the authors are trying to increase the context-dependency scope. Hence, the name of the paper: Transformer-XL Attentive Language Models Beyond a Fixed-Length Context. A simple comparison between Transformer-XL and GPT and BERT can be summarized in the following figure:

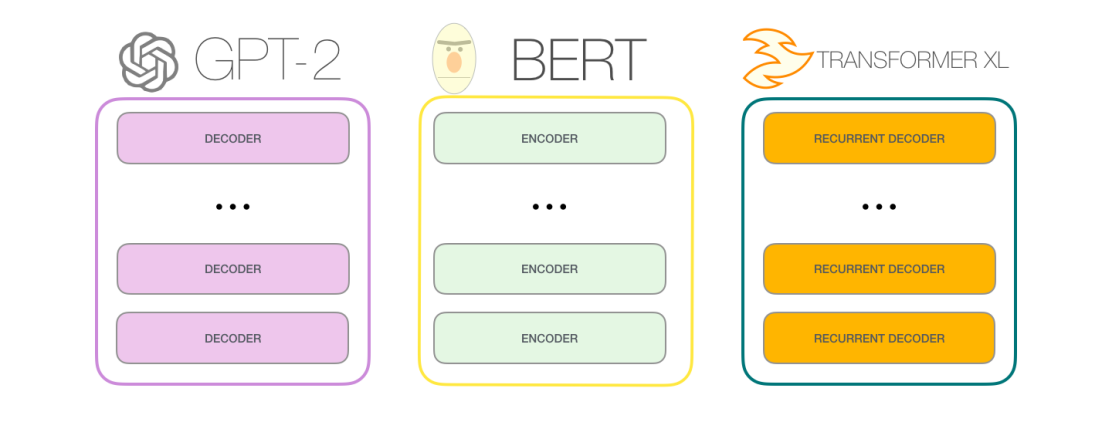
In the transformer architecture, we split the input paragraph into sentences, each sentence can’t exceed a certain length (it’s 512 in BERT). After splitting the paragraph into sentences or “segments”, then we train our model as shown in the following image where we assume the allowed length is just four:

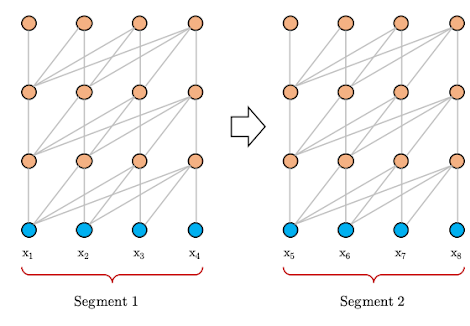
As you can see, segment 2 is after segment 1 in the same paragraph. But according to the transformer architecture, they are totally independent which causes another problem called “context fragmentation” where the model lacks the necessary contextual information to predict the first few symbols due to the way the context was selected. Transformer-XL solves this problem by providing a segment-level recurrence mechanism. And since transformer-XL uses larger context-dependency length, the authors decided to use a different positional encoding than the vanilla transformer.

So, the key innovations behind this paper can be summarized into two things:

  • Segment-level recurrence mechanism.

  • Relative positional encoding scheme.

Segment-level Recurrence

The goal of the recurrence mechanism is to enable long-term dependencies by using information from previous segments. Similarly to the vanilla version, Transformer-XL processes the first segment of tokens but keeps the outputs of the hidden layers. When the following segment is processed, each hidden layer receives two inputs:

  • The output of the previous hidden layer of that segment, as in the vanilla version (the grey arrows in the chart below).

  • The output of the previous hidden layer from the previous segment (the green arrows) that allows the model to create long-term dependencies.

Technically, the two inputs are concatenated and then used to calculate the Key and the Value matrices of the (current Head of the current layer of the) current segment. This addition provides the network with more information in regards to the weights (importance) of each token, but it doesn’t change the Value matrix.

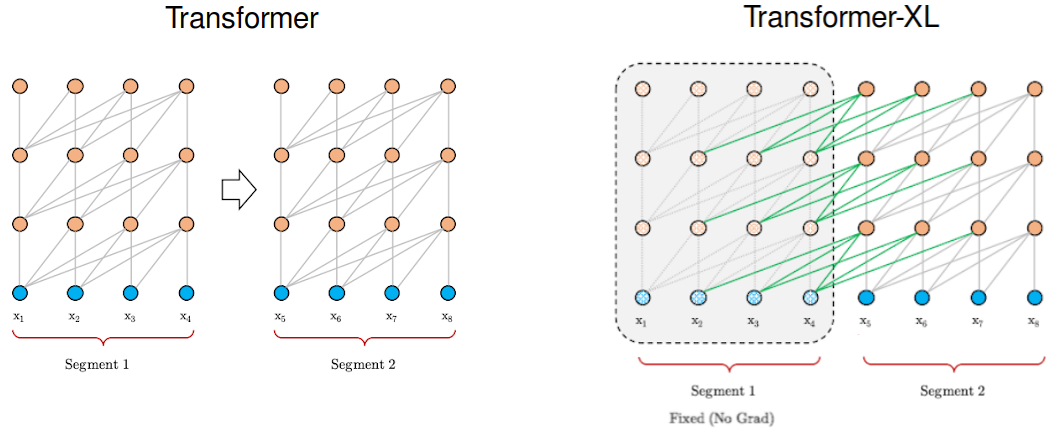
In each segment, each hidden layer receives the output of the previous hidden layer and the output of the previous segment. It increases the largest possible dependency by using contextual information from several previous segments.

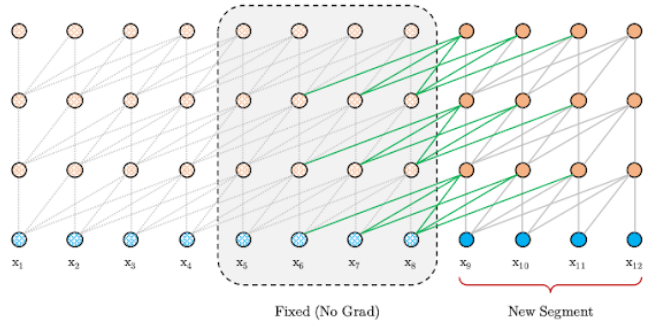
This mechanism can be applied at the decoding step with no problem as shown in the following figure:

Relative Positional Encoding

Naively applying recurrence introduces another technical challenge. That is, the positional information is incoherent, and tokens from different segments have the same positional encoding, which is referred to as temporal confusion. To address this challenge, Transformer-XL employs novel relative positional encodings.

In the vanilla transformer, positional encodings were depending on the index of the tokens. This positional encoding is depending on the relative distance between tokens, hence the name: relative positional encoding. In the paper this was done by expanding the simple query-key multiplication of the Attention Head’s Score.

First, let’s recap what was the query-key multiplication in the attention mechanism of the vanilla transformer:

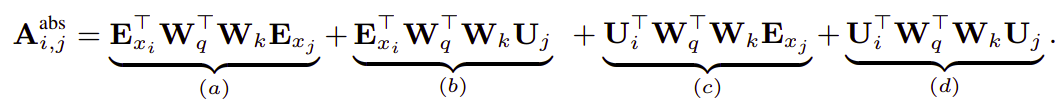
Following the idea of only relying on relative positional information, they proposed to reparameterize the four terms as follows:

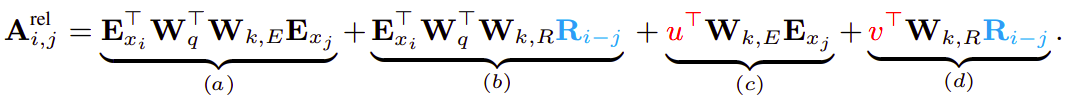
With the following changes:

  • The first change they made is to replace all appearances of the absolute positional embedding $U_{j}$ for computing key vectors in term $(b)$ and $(d)$ with its relative counterpart $R_{i - j}$ . Note that $R$ is a sinusoid encoding matrix without learnable parameters.

  • Secondly, we introduce a trainable parameter $u \in \mathbb{R}^{d}$ to replace the query $U_{i}^{T}W_{q}^{T}$ in term $(c)$. In this case, since the query vector is the same for all query positions, it suggests that the attentive bias towards different words should remain the same regardless of the query position.

  • With a similar reasoning, a trainable parameter $v \in \mathbb{R}^{d}$ is added to substitute $U_{i}^{T}W_{q}^{T}$ in term $(d)$.

  • Finally, we deliberately separate the two weight matrices $W_{k,E}$ and $W_{k,R}$ for producing the content-based key vectors and location-based key vectors respectively.

Under the new parameterization, each term has an intuitive meaning:

  • Term (a): represents content-based addressing.

  • Term (b): captures a content-dependent positional bias.

  • Term (c): governs a global content bias

  • Term (d): encodes a global positional bias.