XLNet
XLNet stands for “Extra-Long Net” which is a model that integrates both GPT and BERT introduced in 2019 by Google Brain and published in this paper: “XLNet: Generalized Autoregressive Pretraining for Language Understanding” by the same authors of Transformer-XL. The official code for this paper can be found in the following GitHub repository: xlnet.
In Transformer-XL, they extended the context-dependency length by introducing the segment-level recurrence mechanism which uses the hidden state of the former segments when predicting the current segment. In this paper, they are trying to make the model uses the hidden state of the former and following segments when predicting the current segment.
And that explains the meaning of the paper’s name. An auto-regressive language model is is a language model that is able to predict the next possible word based on the before-context or predict the previous word based on the after-context. And it’s generalized because it considers both; the before-context and the after-context. The way to do that as proposed by the paper is by using “Permutation Language Modeling”.
PLM
PLM stands for “Permutation Language Modeling” which is the idea of capturing bidirectional context by training an auto-regressive model on all possible permutation of words in a sentence. Instead of a fixed left-right or a right-left modeling, XLNET maximizes expected log likelihood over all possible permutations of the sequence which means that each position will learn to utilize contextual information from all positions thereby capturing bidirectional context.
This mechanism is better than “MLM (Masked Language Modeling)” used with BERT. And that’s because MLM corrupts the input with masks which affects real life applications since we do not have inputs that are masked. Also, MLM ignores the relation between masked tokens. For example, let’s consider this sentence: “She met [mask] and [mask] friends. So, if the first [mask] is “Adam”, then the second [mask] has to be “his”. And this will change when the first [mask] is “Sara” for example.
So, consider a sequence $x = \left[ “This”,\ “is”,\ “a”,\ “sentence” \right]$ with $T = 4$ tokens. Now consider the set of all $4!$ permutations $Z = \left\{ z_{1},\ z_{2},\ …z_{4!} \right\} = {\lbrack 1,\ 2,\ 3,\ 4\rbrack,\ \lbrack 1,\ 2,\ 4,\ 3\rbrack,.\ .\ .,\ \lbrack 4,\ 3,\ 2,\ 1\rbrack}$.
The XLNet model calculates the probability of token $x_{t}$ given preceding tokens $x_{< t}$ from any order which makes the objective function as follows:
\[\max_{\theta}\left( \mathbb{E}_{z\sim Z_{T}}\left\lbrack \sum_{t = 1}^{T}{\log\left( p_{\theta}\left( x_{z_{t}} \middle| x_{z_{< t}} \right) \right)} \right\rbrack \right)\]So, if $t = 3$ and the current permutation is $z = \lbrack 3,\ 2,\ 4,\ 1\rbrack$, it means XLNet will consider zero words $x_{z_{< t}} = \lbrack\rbrack$ when predicting the probability of the third word which corresponds to $p_{\theta}\left( “a” \middle| \varnothing \right)$. While if the current permutation is $z = \lbrack 2,\ 4,\ 3,\ 1\rbrack$, it means XLNet will consider the second and the fourth words $x_{z_{< t}} = \lbrack 2,\ 4\rbrack$ when predicting the probability of the third word which corresponds to $p_{\theta}\left( “a” \middle| “is”,\ “sentence” \right)$.
As you have probably figured out, there is something missing from the way the model has been presented so far: how does the model know about word order? The model can compute $p_{\theta}\left( “This” \middle| “a” \right)$ as well as $p_{\theta}\left( “This” \middle| “is” \right)$. Ideally it should know something about the relative position of “This” and “is” and also of “a”. Otherwise it would just think all tokens in the sequence are equally likely to be next to one-another. And that’s what the attention mask does!
Attention Mask
The transformer architecture addresses this problem by adding masking/zeroing the words that are not in the provided context. As a concrete example, consider the following permutation $z = \lbrack 3,\ 2,\ 4,\ 1\rbrack$. When calculating the probability of the $1^{st}$ element in that order, the model has no context as the other tokens have not yet been seen. So the mask would be $\lbrack 0,\ 0,\ 0,\ 0\rbrack$ as shown below:

For the 2nd element (token 2), the mask is $\lbrack 0,\ 0,\ 1,\ 0\rbrack$ as its only context is token 3. Following that logic, the $3^{rd}$ and $4^{th}$ elements (tokens 4 and 1) have masks $\lbrack 0,\ 1,\ 1,\ 0\rbrack$ and $\lbrack 0,\ 1,\ 1,\ 1\rbrack$ respectively as shown in the following figures:

Another way to look at this is that the training objective will contain the following terms in case of the $z = \lbrack 3,\ 2,\ 4,\ 1\rbrack$ permutation; where underscores represent what has been masked:
\[p_{\theta}\left( "a" \middle| \_\_,\ \_\_,\ \_\_,\ \_\_ \right)\] \[p_{\theta}\left( "is" \middle| \_\_,\ \_\_,\ "a",\ \_\_ \right)\] \[p_{\theta}\left( "sentence" \middle| \_\_,\ "is",\ "a",\ \_\_ \right)\] \[p_{\theta}\left( "This" \middle| \_\_,\ "is",\ "a",\ "sentence" \right)\]But wait a minute! There remains one oversight to address: As you can see, the probability of “sentence” in $4^{th}$ position the previous permutation should be different than when “sentence” is in the $1^{st} position. In other words, we need to use the current word position when calculating the probability; like so:
\[p_{\theta}\left( "sentence" \middle| \_\_,\ "is",\ "a",\ 4 \right)\]And this paper deals with problem by providing a “two-stream” self attention mechanism.
Two-stream Self-Attention
The solution to this problem is a two-stream self-attention mechanism; where the standard self-attention is divided into two parts or streams:
-
Content Stream: The content stream (denoted by $h$) cares about the context of the preceding tokens including the current token, in other words the “content’.
-
Query Stream: The query stream (denoted by $g$) cares about the context of the preceding tokens including the position of the current token.
The following figure shows just two layers of this two-stream self-attention:

Content Stream
The content vector of a token at position $i$ and at self-attention layer $m$ is denoted by $h_{i}^{m}$. All content stream vectors are initialized with token embeddings. It’s calculated according to the following formula:
\[p_{\theta}\left( x \middle| x_{z_{< t}} \right) = \frac{\exp\left( {e(x)}^{T}.h_{\theta}\left( x_{z_{< t}} \right) \right)}{\sum_{x'}^{}{\exp\left( {e(x')}^{T} \right).h_{\theta}\left( x_{z_{< t}} \right)}}\]Where:
-
$x$: is the current token at position $t$ in the current permutation$z$.
-
$e(x)$: is the word embedding of the current token.
-
$x_{z_{< t}}$: is the preceding tokens to the current one.
-
$h_{\theta}\left( x_{z_{< t}} \right)$: denotes the hidden representation of $x_{z_{< t}}$ produced by the shared Transformer network after proper masking.
Considering the $z = \lbrack 3,\ 2,\ 4,\ 1\rbrack$ permutation, at each layer, the content vector $h_{i}$ is updated using the other context vectors that remained unmasked and itself. Thus, $h_{1}$ is updated with the knowledge of $x_{3}$, $x_{2}$ , $x_{4}$ and $x_{1}$ as shown in the following figure:
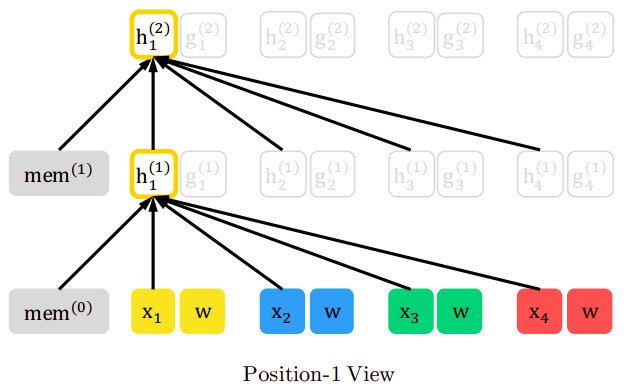
And the following figure shows that all content vectors are contributing in calculating the key-value pair in the attention mechanism, while the current content vector is used for the query vector of the attention mechanism.

Note:
The content stream is the same as the standard self-attention found in the vanilla transformer architecture.
Query Stream
The query vector of a token at position $i$ and at self-attention layer $m$ is denoted by $g_{i}^{m}$. All query stream vectors are initialized with a generic embedding vector $w$ added to positional embeddings. Note that $w$ is the same no matter the token. It’s calculated according to the following formula:
\[p_{\theta}\left( x \middle| x_{z_{< t}} \right) = \frac{\exp\left( {e(x)}^{T}.g_{\theta}\left( x_{z_{< t}},\ z_{t} \right) \right)}{\sum_{x'}^{}{\exp\left( {e(x')}^{T} \right).g_{\theta}\left( x_{z_{< t}},\ z_{t} \right)}}\]Where:
-
$x$: is the current token at position $t$ in the current permutation $z$.
-
$e(x)$: is the word embedding of the current token.
-
$x_{z_{< t}}$: is the preceding tokens to the current one.
-
$g_{\theta}\left( x_{z_{< t}},\ z_{t} \right)$: denotes the hidden representation of $x_{z_{< t}}$ produced by the shared Transformer network after proper masking which additionally take the target position $z_{t}$ as input.
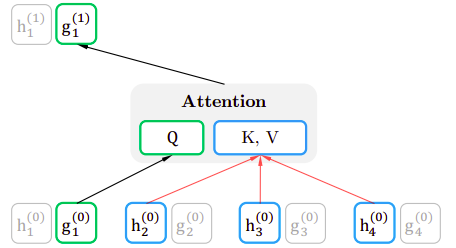
Considering the same permutation in the content stream $z = \lbrack 3,\ 2,\ 4,\ 1\rbrack$, at each layer, the query vector $g_{i}$ is updated using the other context vectors that remained unmasked and itself. Thus, $h_{1}$ is updated with the knowledge of $x_{3}$, $x_{2}$ , $x_{4}$ and $w_{1}$ without considering $x_{1}$ as shown in the following figure:

And the following figure shows that all content vectors (except the current one) are contributing in calculating the key-value pair in the attention mechanism, while the current query vector is used for the query vector of the attention mechanism.