Linformer: Linear Transformer
Linformer is an efficient version of the transformers proposed by Facebook AI in 2020 and published in this paper: “Linformer: Self-Attention with Linear Complexity”. The official code for this paper can be found in the FairSeq official GitHub repository: linformer. Linformer can perform the self-attention mechanism in the transformer in linear time $O\left( n \right)$ instead of a quadratic time $O\left( n^{2} \right)$ in both time and space. In this paper, the publishers demonstrate that the self-attention mechanism can be approximated by a low-rank matrix.
Recap
The Transformer is built upon the idea of Multi-Head Self-Attention which allows the model to jointly attend to information at different positions from different representation sub-spaces. The multi-head self-attention is defined as:
\[\text{MultiHead}\left( Q,\ K,\ V \right) = Concat\left( \text{head}_{1},...\text{head}_{h} \right)\ W^{O}\]Where $Q,\ K,\ V \in \mathbb{R}^{n \times d_{m}}$ are input embedding matrices, $n$ is sequence length, $d_{m}$ is the embedding dimension, and $h$ is the number of heads. Each head is defined as:
\[\text{head}_{i} = \text{Attention}\left( QW_{i}^{Q},KW_{i}^{K},VW_{i}^{V} \right) = \text{softmax}\left\lbrack \frac{QW_{i}^{Q}\left( KW_{i}^{K} \right)^{T}}{\sqrt{d_{k}}} \right\rbrack VW_{i}^{V}\]Where $W_{i}^{Q},W_{i}^{K} \in \mathbb{R}^{d_{m} \times d_{k}}$, $W_{i}^{V} \in \mathbb{R}^{d_{m} \times d_{v}}$, and $W_{i}^{O} \in \mathbb{R}^{\text{hd}_{v} \times d_{m}}$ are learned matrices and $d_{k},d_{v}$ are the hidden dimensions of the projection sub-spaces. The term highlighted in red is the self-attention which is also called “context mapping matrix” denoted $P \in \mathbb{R}^{n \times n}$. Usually, we set $d_{k}$ and $d_{v}$ to be the same size $d$.
The Transformer uses $P$ to capture the input context for a given token, based on a combination of all tokens in the sequence. However, computing $P$ is expensive. It requires multiplying two $n \times d$ matrices, which is $O\left( n^{2} \right)$ in time and space complexity. This quadratic dependency on the sequence length has become a bottleneck for Transformers.
Self-Attention is Low Rank
Based on some analysis including singular value decomposition, the distributional
Johnson–Lindenstrauss lemma (JL for short), and the Eckart–Young–Mirsky Theorem they found out that the self-attention matrix $P$ can be approximated to:
\[P \approx \sum_{i = 1}^{k}{\sigma_{i}u_{i}v_{i}^{T}} = \begin{bmatrix} \ & \ & \ \\ u_{1} & \text{...} & u_{k} \\ \ & \ & \ \\ \end{bmatrix}\text{diag}\begin{Bmatrix} \sigma_{1} & \text{...} & \sigma_{k} \\ \end{Bmatrix}\begin{bmatrix} \ & v_{1} & \ \\ \ & \vdots & \ \\ \ & v_{k} & \ \\ \end{bmatrix}\]where $\sigma_{i}$ , $u_{i}$ and $v_{i}$ are the $i$ largest singular values and their corresponding singular vectors. This performs the self-attention is $O\left( \text{nk} \right)$ time complexity.
In the paper, they optimized the operation from $O\left( \text{nk} \right)$ to $O\left( n \right)$ by projecting two linear projection matrices $E_{i},F_{i} \in \mathbb{R}^{n \times k}$ when computing key and value. So, the self-attention mechanism becomes:
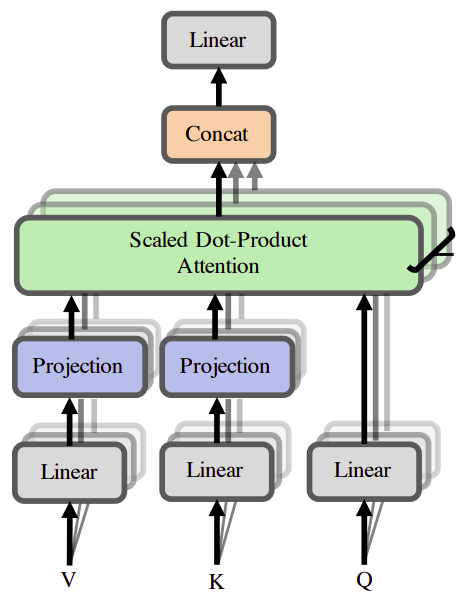
The method included a lot of maths and a lot of theorems. It didn’t make sense to me.
TO BE CONTINUED!