GloVe

GloVe (Global Vectors for Word Representation) is a model released in 2014 by Stanford NLP Group researchers Jeffrey Pennington, Richard Socher, and Chris Manning for learning word embedding and published in the paper: GloVe: Global Vectors for Word Representation. The GloVe authors present some results which suggest that their model is competitive with Google’s popular word2vec package.

The key idea behind GloVe model is to combine two concepts into one model; It learns word vectors by using the same idea of Word2Vec model beside examining [word co-occurrences within a text corpus.

Co-occurrence Matrix

Before we train the actual model, we need to construct a co-occurrence matrix $X$, where a cell $X_{\text{ij}}$ represents how often the word $i$ appears in the context of the word $j$ using a certain window size. We run through our corpus just once to build the window-based co-occurrence matrix $X$ whose dimension is $\left| V \right| \times \left| V \right|$. We will construct our model based only on the values collected in $X$. So, assuming that our corpus has only three sentences which are “I like deep learning.”, “I like NLP.”, and “I enjoy flying.” and assuming also that we have a window of just one word; then our co-occurrence matrix would be:

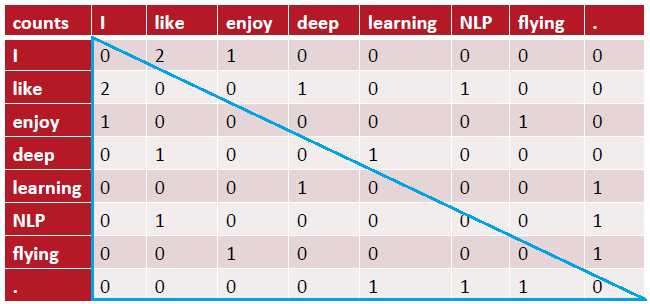
There are a lot of things we should notice looking at this matrix:

• The co-occurrence matrix is symmetric, which means that the co-occurrence count of “I” and “like” is the same as the co-occurrence count of “like” and “I”.

• The shape of the matrix is $V \times V$ where $V$ is the size of the vocabulary which is $8$ in our case here. So, imagine using a million-word vocabulary.

• There are a lot of zeros in this matrix. So, most of the used storage will be just zeros.

To be able to use this matrix in our GloVe model, there are some hacks that we need to do to this matrix:

• Words like “the”, “he”, “she”, “and” …etc. are too frequent, so we can limit their count to a certain number, say $100$, or just ignore them all.

• Use Pearson correlations instead of counts, then set negative values to $0$.

• Ramped windows that count closer words more.

Model

As I said before, GloVe models combine Word2Vec model with the co-occurrence matrix. So, we can imagine that the GloVe model is a modification of the Word2Vec model where we use the word-by-word co-occurrence matrix with word-vectors that we want to train just like that:

Where

• $i$ and $j$ are the word-pairs.

• $X_{\text{ij}}$ refers to the co-occurrence count of word $i$ with word $j$.

• $w_{i}$ and $w_{j}$ are the two word-vectors that we are trying to learn.

• $b_{i}$ and $b_{j}$ are the biases that we are trying to learn as well.

This formula works well, but we can weigh words differently to derive more flexibility and robustness like so:

Such as that:

• $\left| V \right|$ is the number of word-pairs in the vocabulary.

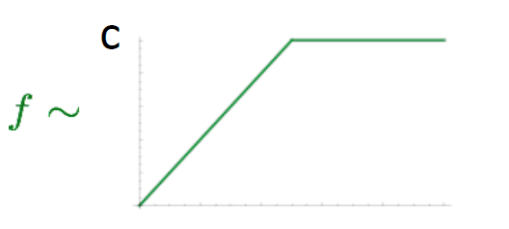
• $f\left( X_{\text{ij}} \right)$ represents a simple function that restrict the values of the co-occurrence count. We can use the following function:

Where $x_{\max}$ is called “the cutoff” usually equals to $100$. When we encounter extremely common word pairs (where $X_{\text{ij}} > x_{\max}$), this function will simply return $1$. For all other word pairs, it will return some weight in the range $\left( 0,1 \right)$, where the distribution of weights in this range is decided by $\alpha$ which is usually equals to $0.75$.

OR we could use a simpler function like the $\max\left( X_{\text{ij}},c \right)$ where $c$ is a constant number (usually $100$).

Evaluation

Before talking about how to evaluate our model, let’s first take about the hyper-parameters that can be tuned to get better and better results. The following graph is from the published GloVe paper:

• First, Same hyper-parameters as Word2Vec models which are:

  • Initialization method.

  • Learning rate $\alpha$.

  • Word vector dimension $d$. Best value for $d$ is about $300$ and it slightly drops-off afterwards. But, it might be different for downstream tasks.

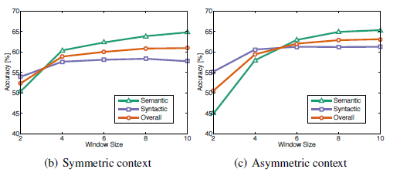
  • Window size $m$. As we can see in the following graph, the best value is around $8$.

  • Using symmetric or Asymmetric windows. Symmetric is using the window size for both directions (left and right). Asymmetric is using the window size for just one direction.

• Using either co-occurrence count or the Pearson correlations instead of counts and set negative values to $0$.

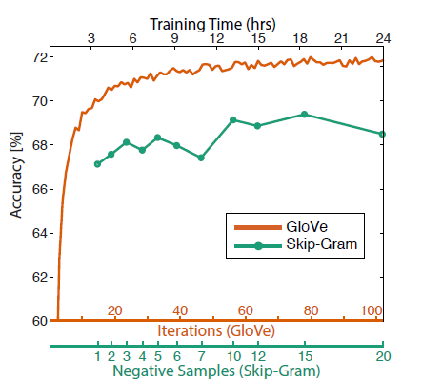
• Training Time (no. of iterations): Usually the more … the better

Now, how to evaluate our model? Let’s first talk about how to evaluate NLP tasks in general. Actually, there are two methods (Intrinsic and Extrinsic). Intrinsic methods try to find a mathematical formula or a sub-task to evaluate our model. While Extrinsic methods try to get our model into a real-life task. Both have some pros and cons:

So, let’s explain this in more details… Assume that we have a word-vectors for a $1,000,000$ word vocabulary and we want to evaluate if these word-vectors are worth publishing or not?? When thinking about intrinsic evaluation, we might think to get just a $10,000$ words and test on a word analogy task]. This is fast to compute, and we can tune some of the parameters to get better and better results. But, $10,000$ isn’t enough, we need to get the whole matrix into consideration. So, we decided to use the whole $1,000,000$ words into the same task (word analogy). Putting in mind that such a task might take hours and hours to train and evaluate. And the results might get worse as the hyper-parameters that we have tuned are for the $10,000$ task not the whole corpus.

So, the solution is to to balance between these two methods. At first, we have to start with the intrinsic method and change only one parameter. And don’t confirm this change unless it’s evaluated by the Extrinsic method.

Note:
We can use a pre-trained GloVe word embedding freely from the Stanford GloVe official website. We can know a lot about these pre-trained models from the name, for example the pre-trained model “glove.6B.50d”, it’s called 6B because it’s formed using 6 billion words in context, and 50d because the extracted features (dimension) are 50.

Re-training Word Vectors

We can always use pre-trained word vectors whether it’s Word2Vec embeddings or GloVe embeddings, but what about use these pre-trained word vectors as the initial weights of our model?? Is it a good idea??

Actually, that’s a great question and the answer is not that simple. But luckily there is a rule-of-thumb that we can use… if the training dataset is quite small, then it’s so much better if we don’t train our model using these pre-trained vectors. And if the training dataset is very large, it may work better to train the model using the pre-trained vectors. And that’s because if the dataset is quite small, some of the word vectors will get better values but not all of them, so the model loses generalization.

Let’s see how… assume that we have a small data corpus where the word “TV” and “telly” are mentioned and the word “television” is not; then when training the model using these small dataset, the model changes the “TV” and “telly” word vectors according to their context. But what about the word “television"?? It won’t change, which makes its vector less similar to the vectors of “TV” and “telly” putting in mind that these three words are the same. So, their pre-trained vectors are pretty similar. That’s why when training a model with small dataset some of the words are left out, and similar word-vectors becomes less similar.