De-biasing Word Vectors

In this paper: Man is to Computer Programmer as Woman is to Homemaker? Debiasing Word Embeddings published in 2016, the researchers examined the gender biases that can be reflected in a word embedding and explore some algorithms for reducing the bias.

First, what does biasing of word vectors really mean? OK, let’s put it that way. There are some words that relate only the females like “actress, waitress, mother, aunt, …” and there are some words that relate only the males like “actor, waiter, father, uncle, …”. And there some other words that can relate to the two genders like “programmer, developer, assistant, doctor, …”.

Surprisingly, most of the word embedding that are out there are biasing towards a certain gender due to the context they were mentioned at. Let’s see the “glove.6B.50d.txt” for example, there are some words that relate to the female more that the male like “lipstick, arts, literature, doctor, receptionist, fashion, …”. And let’s be honest, some of them make perfect sense like “lipstick” for example, but there are also some of them that don’t make any sense like “doctor” and “receptionist” which must be gender unspecific.

We'll see how to reduce the bias of these vectors, using an algorithm due to Boliukbasi 2016. Note that some word pairs such as "actor"/"actress" or "grandmother"/"grandfather" should remain gender specific, while other words such as "receptionist" or "technology" should be neutralized, i.e. not be gender-related. You will have to treat these two types of words differently when de-biasing.

Implicit Association Test

Implicit Association Test is the test used to check if two sets of words are biased towards a certain topic or not. And that’s how it works; assume that you have two sets of words that you want to check the bias between them (they are called attributes):

• X: {male, man, boy, brother, he, him, his, son}.

• Y: {female, woman, girl, sister, she, her, hers, daughter}.

Now, let’s assume that we have another two sets of words that represent two opposing topics (they are called target words):

• A: {math, algebra, geometry, calculus, equations, numbers}.

• B: {poetry, art, dance, literature, novel, symphony, drama}.

And this can be done via the following formula:

Where:

• $s\left( X,Y,A,B \right)$: is the association test between all words of attributes and target words. And it could have three possible values:

  • If the score is positive, it means the association between X and A is big than Y and B. and the higher the score is, the more association there is.

  • If the score is negative, it means the association between Y and B is big than X and A. and the lower the score is, the more association there is.

  • If the score is zero, it means there are no association between X and A and Y and B.

• $s\left( w,A,B \right)$: is the association strength between word w and set A and away from set B.

• $\text{card}\left( A \right)$: It’s the cardinality a set of words A which is a measure of a set's size, meaning the number of unique elements in that set. For instance, the set $A = { 1,2,4}$ has a cardinality of $3$ for the three elements that are in it.

Neutralization

By neutralization, we mean to neutralize the bias for non-gender specific words. So, the words like “receptionist, doctor, literature, art, technology, …” will be gender unspecific. We are going to do that using some linear algebra concepts like so:

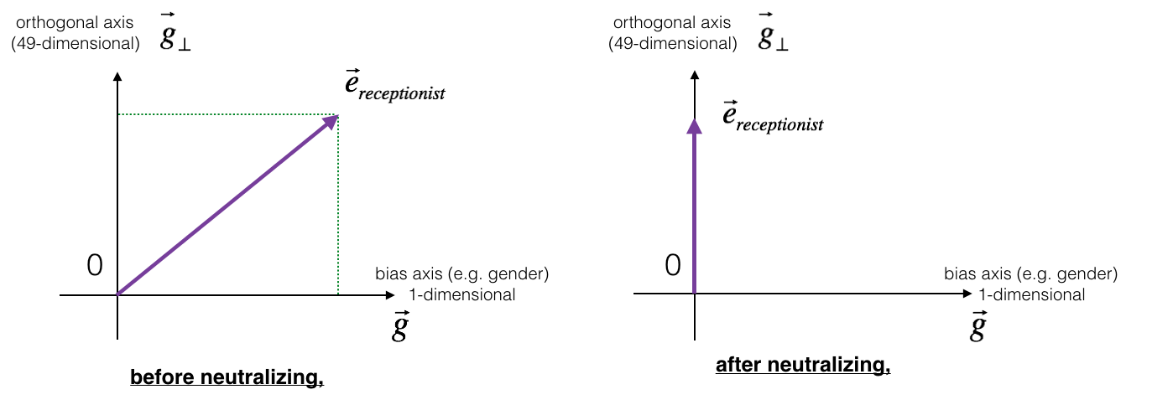
The figure above should help visualizing what neutralization does. If you're using a 50-dimensional word embedding, the 50-dimensional space can be split into two parts: The gender-direction $\overrightarrow{g}$, and the remaining 49 dimensions, which we'll call ${\overrightarrow{g}}_{\bot}$. Even though ${\overrightarrow{g}}_{\bot}$ is 49 dimensional, given the limitations of what we can draw on a screen, we illustrate it using a 1-dimensional axis below.

In linear algebra, we say that the 49-dimensional vector ${\overrightarrow{g}}_{\bot}$ is perpendicular (or “orthogonal”) to $\overrightarrow{g}$, meaning it is at can NOT be affected by $\overrightarrow{g}$ . The neutralization step takes a vector such as $e_{\text{receptionist}}$ and zeros out the component in the direction of $\overrightarrow{g}$ , giving us $e_{\text{receptionist}}^{\text{debiased}}$.

Where $e_{w}$ is the word embedding of a certain word $w$, $g$ is the gender direction, $e_{\text{proj}}$ is the projection of $e_{w}$ onto the direction $g$ and finally $e_{\text{debiased}}$ is the de-biased form of $e_{w}$.

Let’s implement a function which can remove the bias of a given word:

def project(A, B):
    return (np.dot(A, B) / np.sum(B**2)) * B

def neutralize(word, g, word_embedding):
    e_w = word_embedding[word]
    e_proj = project(e, g)
    e_debiased = e_w - e_proj
    return e_debiased

Now, we can try:

>>> # we can get the gender vector by simply doing so:
>>> g = embedding['women'] - embedding['man']
>>> # cosine similarity before neutralizing:

>>> cosine_similarity(embedding['receptionist'], g))
0.330779417506

>>> e_debiased = neutralize("receptionist", g, embedding)
>>> # cosine similarity after neutralizing:
>>> cosine_similarity(e_debiased, g))
-3.26732746085e-17

Equalization

By equalization, we mean to equalize the values of gender-specific words like “(actress, actor), (father, mother), …”. Equalization is applied to pairs of words that you might want to have differ only through the gender property. As a concrete example, suppose that "actress" is closer to "babysit" than "actor." By applying neutralizing to "babysit", we can reduce the gender-stereotype associated with babysitting. But this still does not guarantee that "actor" and "actress" are equidistant from "babysit." The equalization algorithm takes care of this.

The key idea behind equalization is to make sure that a particular pair of words are equi-distant from the 49-dimensional vector ${\overrightarrow{g}}_{\bot}$. In pictures, this is how equalization works:

The derivation of the linear algebra to do this is a bit more complex, but the key equations are:

Let’s get to the implantation:

def equalize(pair, bias_axis, word_to_vec_map):
    w1, w2 = pair
    e_w1, e_w2 = word_to_vec_map[w1], word_to_vec_map[w2]
    mu = (e_w1 + e_w2) / 2.
    mu_B = project(mu, bias_axis)
    mu_orth = mu - mu_B
   
    e1_orth = mu_orth
    e2_orth = mu_orth
    
    e_w1B = np.sqrt(np.abs(1 - normalize(mu_orth)**2))\
                * (project(e_w1, bias_axis) - mu_B) \
                / np.linalg.norm(np.abs(project(e_w1, bias_axis) - mu_B))

    e_w2B = np.sqrt(np.abs(1 - normalize(mu_orth)**2)) \
                * (project(e_w2, bias_axis) - mu_B) \
                / np.linalg.norm(np.abs(project(e_w2, bias_axis) - mu_B))
    
    e1 = e_w1B + e1_orth
    e2 = e_w2B + e2_orth
    return e1, e2

Now, let’s see it in action

>>> # cosine similarities before equalizing:
>>> cosine_similarity(embedding['man'], g))
-0.117110957653

>>> cosine_similarity(embedding['man'], g))
0.356666188463

>>> e1, e2 = equalize(('man', 'woman'), g, embedding)
>>> # cosine similarities after equalizing:
>>> cosine_similarity(e1, g))
-0.700436428931

>>> cosine_similarity(e2, g))
-0.700436428931