Sentence Embedding

Here, we are going to talk about an important issue that tried to use the Word Embedding to produce a sentence embedding. By sentence embedding, we mean to provide a vector of $d$ length that has the meaning of the sentence in a numerical form; the same form as we did with word embedding.

Following this approach, we could be able to found similarity between two sentences that has similar meaning. And this could give us some superiority over Cosine Similarity which determines the similarity bases on the common words. Using two sentences like “Mexico wishes to guarantee citizen’s safety” and “Mexico intends to avoid more violence” will be not that similar using Cosine Similarity even though they are pretty similar in the meaning. And two sentences like “Iranians Vote in Presidential Election” and “Keita Wins Mali Presidential Election” will be very similar using cosine similarity although they are not similar in the meaning.

Le and Mikolov from Google, in their paper: “Distributed Representations of Sentences and Documents” published in 2014, proposed different techniques for Sentence Embedding as we are going to discuss below:

Bag-of-Words (BoW)

This is the simplest method of which we can covert the word embedding vectors into sentence embedding vector. In this method we get the average of the words vectors that form the sentence. So, the sentence embedding vector of “Natural Language Processing” is:

But this method neglects a lot of information like the sequence of the words and that might give false results. So, for example the sentence “You are going there to teach not to play.” will have the same sentence embedding as “You are going there to play not to each.” even though they are exactly the opposite.

Distributed Bag-of-Words (DBoW)

Le and Mikolov from Google, in their paper “Distributed Representations of Sentences and Documents” published in 2014, proposed an distributed bag-of-words (DBOW) which used only the paragraph context vector to predict the words in the paragraph. This simple model is analogous to the skip-gram version of word2vec, except the paragraph vector is used to predict all the words paragraph instead of using the target word to predict the context words. As in the skip-gram model, DBOW is very computationally and memory efficient. Empirical results have shown that both DM and DBOW outperform bag-of-words and bag-of-n-gram models for text representations. Furthermore, averaging the DM and DBOW vector representations often yields the best performance overall.

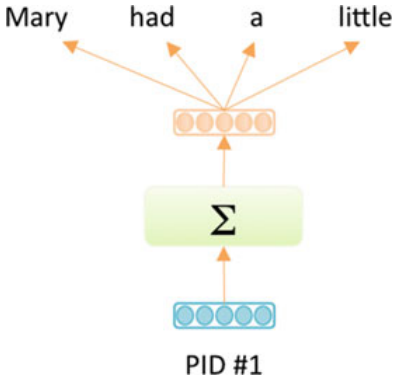
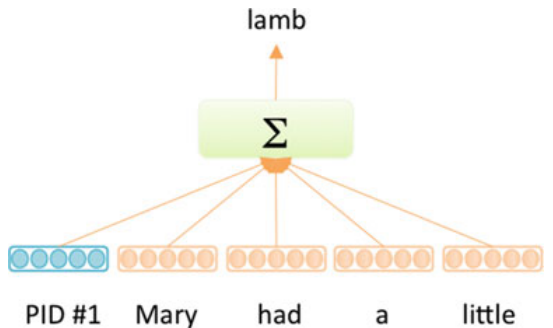
doc2vec

The model generates fixed-length feature representations from variable length pieces of text, making it useful for application to sentences, paragraphs, sections, or entire documents. The key to the approach is to associate every paragraph with a unique paragraph vector $u^{i}$, which is averaged with the word vectors $w_{j}^{i}$ of the $J$ words in the paragraph to yield a representation of the paragraph $p^{i}$:

The paragraph vector ui can be thought of acting as a memory that remembers word order context. During training, a sliding window of context words $C$ and the paragraph vector $p^{i}$ are used to predict the next word in the paragraph context. Both paragraph vectors and word vectors are trained via backpropagation. While the paragraph vector is unique to each paragraph and shared across all contexts generated from the same paragraph, the word vectors are shared across the entire corpus. It is notable that the

Later Check:

There is a famous paper published by Sanjeev Arora, Yingyn Liang, and Tengyu Ma, who are a group of researchers at Princeton, and they call it “A simple but Tough-to-beat Baseline for Sentence Embedding”.