Luna: Linear Attention Mechanism
Luna stands for “Linear Unified Nested Attention” which is a novel attention mechanism that yields linear time and space complexity as opposed to standard attention mechanism proposed in the Transformer architecture that yields quadratic time and space complexity. Luna was proposed by FAIR in 2021 and published in the paper under the same name: “Luna: Linear Unified Nested Attention”. The official code for this paper can be found in the following GitHub repository: fairseq-apollo.

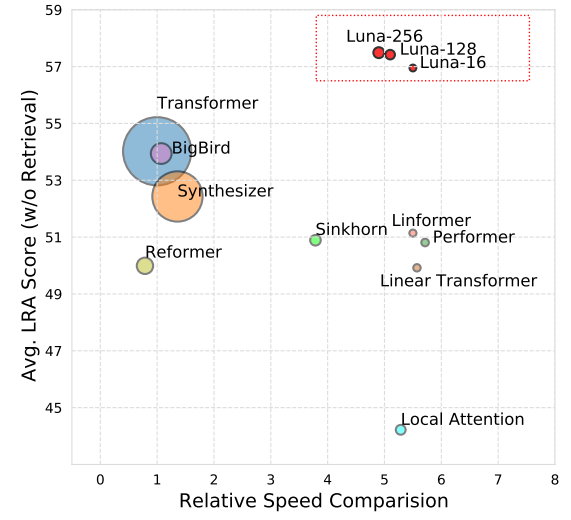
As compared to other attention mechanism proposed by different models, Luna achieves competitive or even better performance, while acquiring prominent gains of efficiency in both speed and memory as shown in the following figure:
Attention Recap
Before getting into Luna details, let’s first recap the attention mechanism. The traditional attention mechanism is a function of two sequences: the query sequence $X \in \mathbb{R}^{n \times d}$ with length $n$ and the context sequence $C \in \mathbb{R}^{m \times d}$ with length $m$. And it outputs one sequence $Y \in \mathbb{R}^{n \times d}$ with the same length as the query $X$:
\[Y = \text{Attention}\left( X,\ C \right) = \text{softmax}\left( \frac{XW^{Q}\left( CW^{K} \right)^{T}}{\sqrt{d}} \right)CW^{V}\]Where $d$ is the embedding dimension, and $W^{Q},W^{K},W^{V} \in \mathbb{R}^{d \times d}$ are three learnable parameters that project the input sequences into the space of query, key and value matrices: $Q = XW^{Q},\ K = CW^{K},\ V = CW^{V}$ respectively. Each head in the multi-head attention mechanism has different learnable parameters.
Note:
In self-attention mechanism, $X = C$, where both come from either the encoder or the decoder. In cross-attention, $X$ comes from the encoder and $C$ comes from the decoder.
The matrix $\text{softmax}\left( \frac{XW^{Q}\left( CW^{K} \right)^{T}}{\sqrt{d}} \right) \in \mathbb{R}^{n \times m}$ is called the “attention matrix” which specifies the alignment scores between every pair of tokens in sequences of queries $X$ and contexts $C$. Calculating the attention matrix takes $O\left( \text{nm} \right)$ time and space, which is quadratic with respect to the sequence length and becomes a significant bottleneck when processing long sequences.
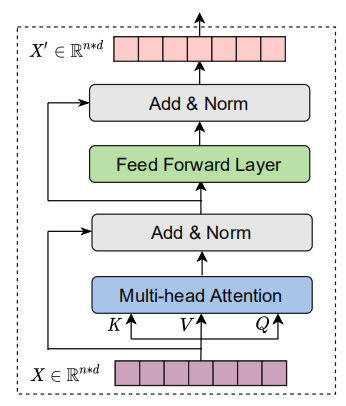
The other two key components of Transformer, besides attention, are feed-forward networks (FFN) and layer normalization. Each Transformer layer can be expressed as:
\[X_{A} = \text{LayerNorm}\left( \text{Attention}\left( X,\ C \right) + X \right)\] \[X' = \text{LayerNorm}\left( \text{FFN}\left( X_{A} \right) + X_{A} \right)\]Where $X’$ is the output of the transformer layer. Here, we used the original post-layer normalization architecture which places layer normalization after the residual connection.
Luna Attention
The key idea behind Luna attention is to decouple the attention function mentioned above into two nested attention operations, both of which have linear efficiency:
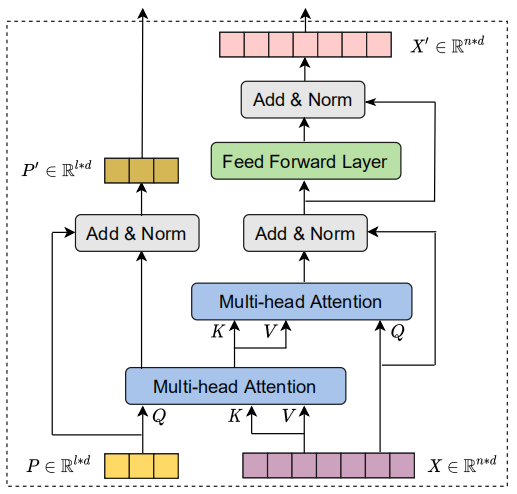
- Pack Attention: Which packs the context sequence $C \in \mathbb{R}^{m \times d}$ into a fixed-length sequence $Y_{P} \in \mathbb{R}^{l \times d}$ with a fixed length $l$ using the standard attention function with $P \in \mathbb{R}^{l \times d}$ as a query sequence (gonna explain where $P$ comes from in a second):
- Unpack Attention: unpacks the sequence $Y_{P} \in \mathbb{R}^{l \times d}$ back to the length of the original query sequence $Y_{X} \in \mathbb{R}^{n \times d}$ using the same standard attention function:
The complexity of pack attention and the unpack attention is $O\left( \text{lm} \right)$ and $O\left( \ln \right)$ respectively which is linear with respect to $m$ and $n$ respectively.
Now, the question is “how to get $P \in \mathbb{R}^{l \times d}$?”. At the first Luna layer, $P$ is created as a learnable positional parameter. At other following layers, $P$ is calculated via the following formula:
\[P^{+} = \text{LayerNorm}\left( Y_{P} + P \right)\]Now, Luna layer, shown in the previous layer, is composed of the following:
\[Y_{X},\ Y_{P} = \text{LunaAttention}\left( X,\ P,\ C \right)\] \[X_{A},\ P_{A} = \text{LayerNorm}\left( Y_{X} + X \right),\ \text{LayerNorm}\left( Y_{P} + P \right)\] \[X',\ P' = \text{LayerNorm}\left( \text{FFN}\left( X_{A} \right) + X_{A} \right),\ P_{A}\]Experiments
To evaluate Luna on sequence-to-sequence modeling, they evaluated it on WMT’14 English-German (EN→DE) machine translation dataset using BPE vocabulary of 37K subwords. The Luna models was closely following the architecture of Transformer-base: 6 encoder and decoder layers with 8 attention heads and model size of 512 and hidden size of 2048.
Unlike the Transformer-base, Luna was trained using Apollo optimizer with learning rate of 0.1, $\beta = 0.9$ , and $\epsilon = 1e^{- 4}$. For learning rate scheduling, they applied linear warm up the first 1000 steps. After learning rate warm up, they decayed the learning rate at the 300,000 and 450,000 steps by decay rate 0.1. Gradient clips with 1.0 were applied. And the dropout ratio are set to 0.1. The weight decay rate was set to $1e^{- 8}$.
The following table presents Luna results in comparison with Transformer models trained using Adam and Apollo optimizers along with Random Feature Attention (RFA) model. We can see that, Luna achieves similar results to the Transformer model. Also, we note that Luna with softplus activation function consistently outperforms ELU.

Note:
When saying Luna-16, we mean Luna where $l = 16$. Here, softplus and ELU activation functions were used instead of the softmax in the attention mechanism.
To evaluate the effectiveness of Luna on long sequences, they trained Luna on the Long Range Arena (LRA) benchmark which consists of five tasks, each designed for the purpose of evaluating Transformer models under the long-context (from 1K to 8K tokens). The following table shows that Luna outperforms baseline models on three out of five tasks and performs comparably with the best performed model on the other two tasks:

Also, Luna was pre-training on Masked Language Modeling (MLM) objective and then fine-tuned on Natural Language Understanding downstream tasks and was found out to have very similar results in comparison with state-of-the-art models such as BERT and RoBERTa:

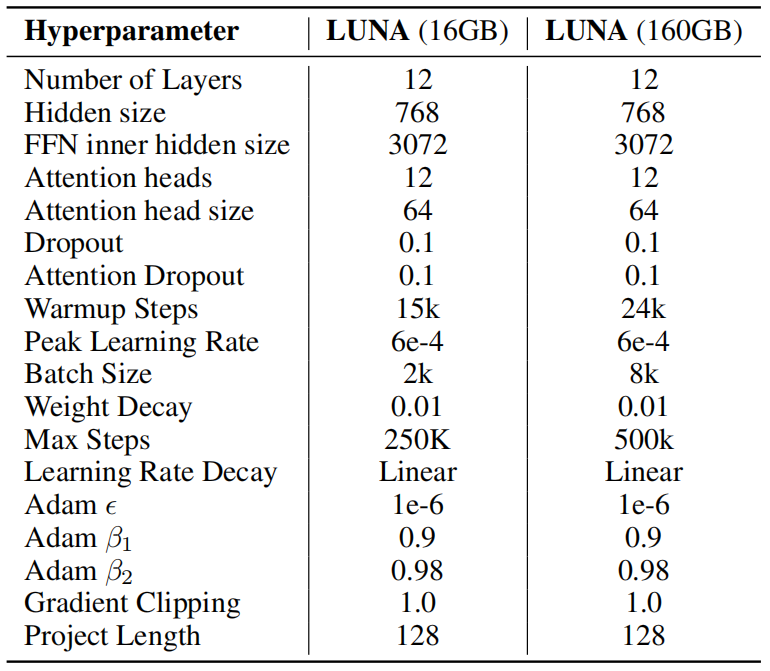
Luna-128 (16GB) was pre-trained on 16GB of monolingual data collected from BookCorpus and English Wikipedia which is the same data used with BERT. Luna-128 (160GB) was pre-trained on 160GB of monolingual data collected from the same sources in addition to CC-News, OpenWebText, and Stories which is the same data used with RoBERTa. The following are the hyper-parameters used for pre-training Luna-128 (16GB and 160GB):