Mohamed Anwar

I'm an ex-AI research resident at Meta

Also, I review research papers in these topics:

5 mins read

Published by: FAIR

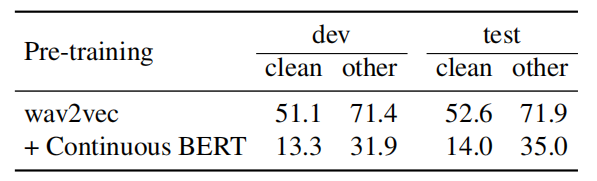
Acoustic BERT

BERT was created as a language model that deals with textual data, However, have you ever wondered if we used BERT on an acoustic data, what will be its performance? Apparently, some researchers at Facebook AI Research in 2019 tried to answer that question and published a paper called “Effectiveness of Self-Supervised Pre-Training for Speech Recognition” where they tried to fine-tune a pre-trained BERT model for speech recognition task using CTC loss function. To enable BERT to deal with input audio data, they tried using two different approaches as shown in the following figure:

  • Discrete BERT: when they used quantized audio representation.

  • Continuous BERT: when they used continuous audio representations.

Note to Reader:
You need to brush-up your information about these topics: BERT, wav2vec, and vq-wav2vec.

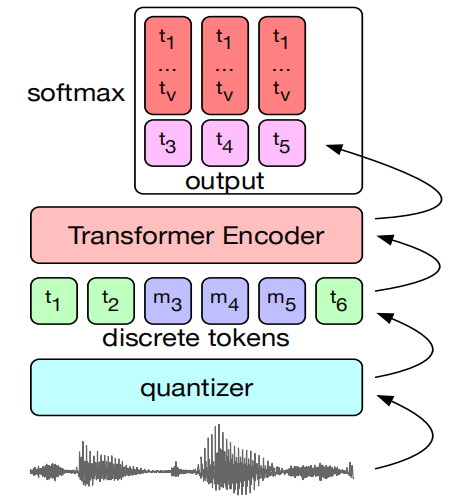
Discrete BERT

Discrete BERT, as shown in the following figure, consists of three different main components:

  • Audio representation: They tried two different audio representations:

    • Mel-frequency Cepstral Coefficients (MFCC).

    • Log-mel Filterbanks (FBANK).

    • Discrete vq-wav2vec features.

  • Quantizer: They used the gumbel-softmax variant proposed in the vq-wav2vec model. They quantized the Librispeech dataset into 13.5k unique codes, to be comparable to vq-wav2vec.

  • Transformer Encoder: These quanitized audio features are passed to a BERT model that was pre-trained with only the masked language modeling task on each set of inputs. Masking was done by choosing tokens for masking with probability of $5\%$, expanding each chosen token to a span of a length sampled from a normal distribution $\mathcal{N}\left( 10,\ 10 \right)$ knowing that spans may overlap. Following “Transformers with Convolutional Context for ASR” paper, they replaced the fixed positional embeddings in the BERT model with a single group convolutional layer. The convolutional layer has a kernel size of $128$ and group size of $16$ to reduce the number of added parameters.

Continuous BERT

Similar to Discrete BERT, Continuous BERT consists of just two main components:

  • Audio Representation: They tried three different audio continuous representations:

    • Mel-frequency Cepstral Coefficients (MFCC).

    • Log-mel Filterbanks (FBANK).

    • Continuous wav2vec features.

  • Transformer Encoder: A BERT’s masked language modeling task cannot be performed with continuous inputs, as there are no targets to predict in place of the masked tokens. To overcome that, they pre-trained BERT to classify the masked positive example among a set of negatives. The model is optimized with the InfoNCE loss where given one positive sample $z_{i}$ and $N$ negative samples $\widetilde{z}$:

\[\mathcal{L}_{k} = \sum_{i = 1}^{T}\left( \frac{\exp\left( z_{i} \right)}{\sum_{j = 1}^{N}{\exp\left( {\widetilde{z}}_{j} \right)}} \right)\]

Where each sample $z_{i}$ is computed as a dot product of the output of the model at timestep $i$ and the true unmasked value of positive example at timestep $i$ or a randomly sampled negative example.

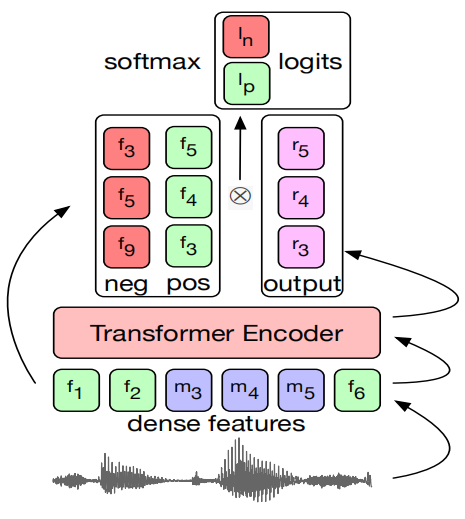
To stabilize training, they added the squared sum of logits produced by the dot-product to the loss, and then apply a soft clamp ${\widetilde{s}}{i} = \lambda tanh\left( \frac{s{i}}{\lambda} \right)$ for each logit $s_{i}$ to prevent the model’s tendency to continually increase the magnitude of logits during training.

Fine-tuning

The Discrete/Continuous BERT were pre-trained on the unlabeled 960h Librispeech data, and then fine-tuned on LibriLight training sets of 100 hours, 10 hours, 1 hour, and 10 mins to perform the speech recognition task using CTC loss; by adding a randomly initialized linear projection on top of the features computed by the transformer models into $V$ classes representing the vocabulary. The vocabulary is 29 tokens for character targets plus a word boundary token.

For data augmentation, they applied SpecAugment during training which delayed overfitting and significantly improved the final accuracy numbers, especially on the smallest subsets. For regularization, they used a dropout at every layer of the transformer of $0.1$ for 10 minute and 1 hour setup, but it was disabled for the 10 hour set and 100 hours. The Libri-light training sets were sampled equally from the two clean and noisy portions, a balance of male and female speakers.

Experiments & Results

The model they used is a standard BERT model with 12 transformer layers, model dimension $768$, inner dimension (FFN) $3072$ and $12$ attention heads. The learning rate is warmed up over the first $10,000$ updates to a peak value of $1 \times 10^{- 5}$, and then linearly decayed over a total of $250k$ updates.

In the first experiment, they compared Discrete BERT and Continuous BERT in different simulated labeled data scenarios ranging from 100 hours to 10 minutes. From this table, we can see the following:

  • Discrete BERT outperforms Continuous BERT in all settings.

  • The best input features are obtained through self-supervised learning through vq-wav2vec for Discrete BERT, or wav2vec for Continuous BERT.

  • When reducing the amount of labeled training data from 100h to 10h results in an increase of only 2 WER on test-other and 1.4 WER on test-clean for Discrete BERT with vq-wav2vec inputs. This shows that pre-training is effective and particularly so when little labeled data is available.

In the second experiment, they compared Discrete BERT to other models. Fine-tuning Discrete BERT on only 10 hour of labeled data can nearly match the best known result on 100 hours of labeled Librispeech data on test-clean, while achieving a 25% relative WER reduction on test-other. Moreover, when using the same train-clean-100 subset for fine-tuning, Discrete BERT with vq-wav2vec inputs improves by 6.5 WER (35% relative WER reduction) on test-other and 1.3 WER (22% relative WER reduction) on test-clean over.

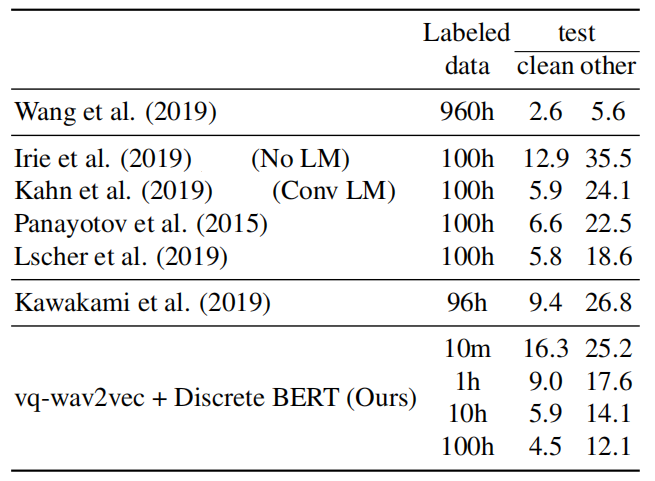
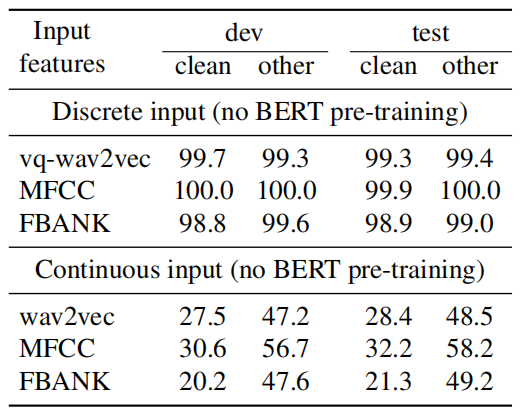
To better understand the impact of BERT pre-training, they decided to remove the BERT pre-training step and only perform unit discovery through vq-wav2vec, for discrete inputs, and fine-tuning, for both discrete and continuous inputs on the 10 hour labeled setup. The following table shows that training with discrete inputs fails. This is likely because the representations of the input discrete units are random and training on the labeled data is not sufficient. Continuous inputs do not suffer from this issue.

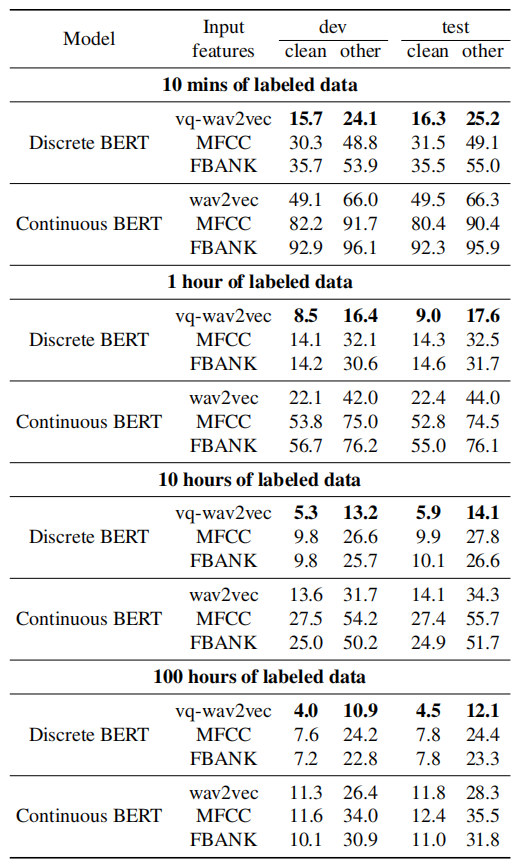
Also, they shed some light on how a two-step pre-training approach compares to a single-step approach. Specifically, they compared Continuous BERT with wav2vec input features to just wav2vec features fine-tuned with a CTC loss on labeled data. The following table shows that Continuous BERT + wav2vec provides substantial gains: