ETC: Extended Transformer Construction
ETC stands for “Extended Transformer Construction” which is a new Transformer architecture for language modeling over long sentences and achieves state-of-the-art performance on various long-sentence tasks as shown in the following table. ETC was proposed by Google in 2020 and published in this paper: “ETC: Encoding Long and Structured Inputs in Transformers”. The official code for this paper can be found on Google Research’s official GitHub repository: research-etc-model .
Many variants of the original Transformer model have been proposed for language modeling such as BERT, RoBERTa, ALBERT, or even T5 limit inputs to $n = 512$ tokens due to the $O\left( n^{2} \right)$ cost of attention. ETC scales to longer input sentences up to $n = 8192$ tokens or more. ETC follows the encoder-side of the original Transformer architecture with three key modifications to tackle long inputs:
-
Relative Position Encoding
-
Global-local Attention.
-
CPC pre-training task.
Relative Position Encoding
Inspired by the work of this paper: Self-attention with relative position representations, ETC replaces absolute position encodings with relative position encodings. There will be $2k + 1$ relative positions given a maximum clipping distance $k$, no matter the length of the input sentence. Given the input sequence $x = \left\{ x_{1},\ …\ x_{n} \right\}$, the relative position between two tokens $x_{i}$ and $x_{j}$ will be:
\[\left\{ \begin{matrix} l_{j - i}\ \ \ \ \ - k < j - i < k \\ l_{- k}\ \ \ \ \ \ \ \ \ \ \ \ \ j - i \leq - k \\ l_{k}\ \ \ \ \ \ \ \ \ \ \ \ \ j - i \geq - k \\ \end{matrix} \right.\]Each relative position then becomes a learnable vector $a_{l}^{K}$, which modifies the attention mechanism as we are going to see later. Now, we can clearly see that these relative position encodings are independent of input length, so it is easy to adapt a model to greater input lengths.
Global-local Attention
Given the input sequence $x = \left\{ x_{1},\ …\ x_{n} \right\}$, ETC model will split it into two separate sequences:
- The long input $x^{l}$: which contains the input that standard Transformer would get.
- The global input $x^{g}$: which is a much smaller number of auxiliary tokens $\left( n_{g} \ll n_{l} \right)$:
Then, attention will be split into four separate pieces: global-to-global (g2g), global-to-long (g2l), long-to-global (l2g), and long-to-long (l2l). Attention in the l2l piece is restricted to a fixed radius as we can see in the following figure (part c); because it is the most computationally expensive part of the whole attention mechanism.
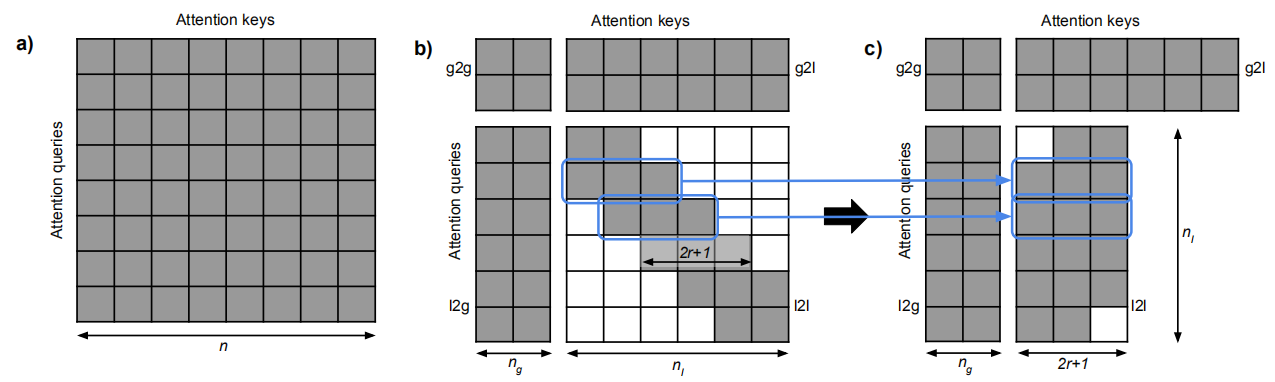
Attention in ETC is $O\left( n_{g}\left( n_{g} + n_{l} \right) + n_{l}\left( n_{g} + 2r + 1 \right) \right)$. Since $n_{l} \gg n_{g},\ r$, then the attention mechanism becomes $O\left( n_{g}^{2} + n_{g}n_{l} \right)$. As we can see, the attention mechanism is linear in the size of the long input . The attention mechanism is applied via the following steps:
-
Per-instance, four Boolean attention matrices $M^{g2g} \in \mathbb{R}^{n_{g} \times n_{g}}$, $M^{g2l} \in \mathbb{R}^{n_{g} \times n_{l}}$, $M^{l2g} \in \mathbb{R}^{n_{l} \times n_{g}}$, and $M^{l2l} \in \mathbb{R}^{n_{l} \times n_{l}}$are created with zeroes for those pairs of tokens that should not attend to one another and ones for the rest.
-
Given the global input $x^{g}$ which is a sequence of token representations $x_{i}^{g} \in \mathbb{R}^{d_{x}}$, a large constant $C = 10,000$ (in the paper), $a_{\text{ij}}^{K}$ learnable vectors representing the relative positions, and $W^{Q},\ W^{K}$ learnable weight matrices, the attention embedding between $x_{i}$ and $x_{j}$ in the global-to-global part can be calculated as:
- A softmax is used to calculate $\alpha_{\text{ij}}^{g2g}$:
- The attention output of the global-to-global part is $z^{g} = \left\{ z_{1}^{g},\ …z_{n_{g}}^{g} \right\}$ where $z_{i}^{g} \in \mathbb{R}^{d_{z}}$ which uses $W^{V}$ as a learnable weight matrix is calculated as follows:
-
Attention for the other 3 pieces is analogous to this one.
-
At the end, a single softmax is used to jointly calculate $\alpha_{\text{ij}}^{g2g}$ and $\alpha_{\text{ij}}^{g2l}$ while another one for $\alpha_{\text{ij}}^{l2g}$ and $\alpha_{\text{ij}}^{l2l}$. I DON’T KNOW HOW :(
-
Thus, the output of global-local attention is a sequence of length $n_{g}$ and one of length $n_{l}$. These sequences go through a layer normalization and feed forward layer in the same way as in the standard transformer.
CPC
ETC model uses two pre-training tasks. The first one is Masked Language Modeling (MLM) with whole word masking which means if one word piece token is masked, then all other tokens of the same word are masked. The second one is Contrastive Predictive Coding (CPC). The goal of CPC is to predict subsequent inputs in latent space, i.e., to predict internal hidden representations of blocks of tokens. We adapted this idea in ETC by using global input sentence summary tokens.
Given an input sequence containing $n$ sentences, we mask all the tokens corresponding to a subset of sentences (but leave the sentence summary tokens in the global input). Then, the model is trained to minimize the difference between the hidden representation of the global sentence summary tokens for the masked sentences with respect to that of a global summary token that can see the unmasked sentence and nothing else. A Noise Contrastive Estimation (NCE) loss is used:
Experiments
ETC model was initialized using RoBERTa parameters. This is doable since BERT’s attention is a special case of the global-local attention used in ETC. Same as RoBERTa, they created two basic configurations:
| Layers | Hidden Size | Attention Heads | # Parameters | $$r$$ | $$k$$ | |
|---|---|---|---|---|---|---|
| Base | 12 | 768 | 12 | 166 M | 84 | 12 |
| Large | 24 | 1024 | 16 | 558 M | 169 | 24 |
For pre-training; they used original BERT datasets, except that documents with fewer than 7 sentences were filtered out with WordPiece vocabulary of 30k uncased wordpieces . ETC-base was pre-trained with the same total number of tokens as the original BERT, while ETC-large was pre-trained with twice as many. As an optimizer, they used LAMB optimizer with learning rate set to $\sqrt{8} \times 10^{- 3}$.
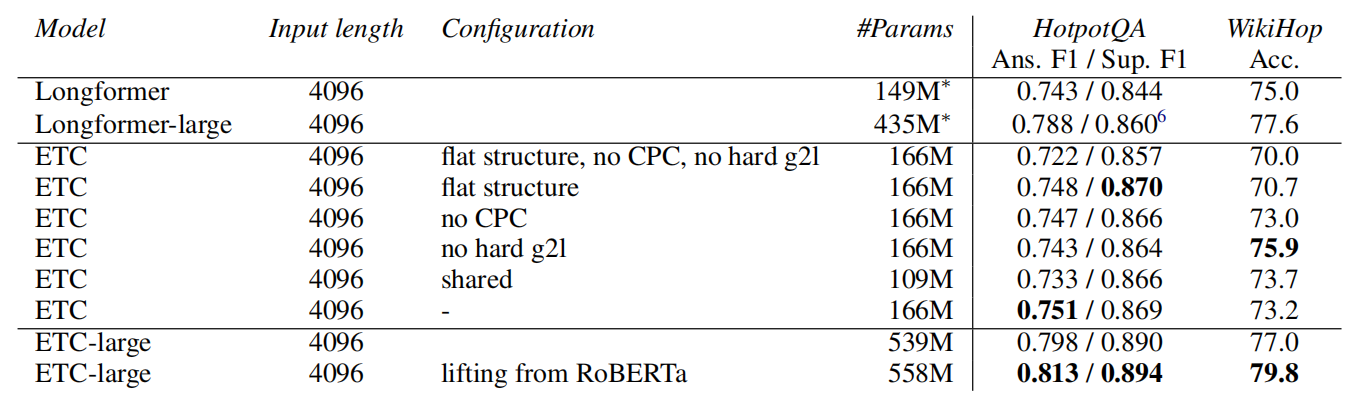
The following are the results obtained by ETC in various benchmarks; the defaulted configuration is marked with “-“:
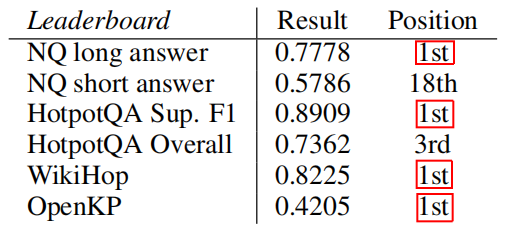
- Natural Questions (NQ):

- OpenKP:

- HotpotQA and WikiHop: